API 510 remaining life: Half-Life VS Double Corrosion Rate principles

4 October 2022 Ali Sassi 0 Comments

API 510 remaining life: Half-Life VS Double Corrosion Rate principles

One of the first objectives of an in-service inspection of pressure vessels is to estimate the remaining life and to set the next planned internal and external intervals. API 510 gives guidance on how to calculate these parameters.

At first look, it seems just a matter of a simple equation where remaining life can be calculated known as the corrosion rate, the current thickness, and the retirement thickness. In the API exam certainly, it is not a complicated question to be answered as in most cases all these parameters are given.

But in reality, it is far more than that. For example, the corrosion rate is not given and the authorized inspector shall estimate it. If erroneous the result of the inspection will be also. Here it is a question of understanding the whole approach rather than just giving a result of an equation. The authorized inspector has the responsibility to pronounce the Vessel’s state. Is it fit to serve? For how long? When the next inspection shall be conducted? Are there any safety issues? Is NDT well performed? Are the NDT results acceptable? Are there any repairs to be performed before start-up?

Many other questions can arise but basically, in terms of remaining life calculation the most important question to be answered by the order are the following:

What approach shall be used when calculating the remaining life (Half-Life or Double Corrosion rate?
Is the corrosion rate adopted correct and reflects the real state of the vessel?

We will try in this article to answer these two questions and detail also some other aspects to be considered when evaluating the remaining life (aspects that API 510 does not clearly explain but are rules of thumb).

I Half-Life VS Double Corrosion Rate principles

I-1 Half-Life principle

If you are an authorized API 510 inspector or intend to sit for the API 510 exam, you must know the Half-life principle adopted by API 510 for setting the internal inspection intervals of in-service pressure vessels. The principle is easy to understand:

Calculate the remaining life of the vessel knowing the corrosion rate, the actual thickness, and the retirement thickness (t_required)

$\frac{t_{actual} – t_{required}}{corrosion rate}$

The Internal inspection interval will be the half remaining life but shall not exceed 10 years
Exceptions for vessels of the remaining life of 04 years and less where internal inspection interval is set to the hole remaining life but not exceeding 02 Years

For the last point, is it complicated? To simplify, it means that if the remaining life is between 04 and 02 years the inspection interval is 02 years otherwise for vessels with a remaining life of fewer than 02 years the inspection interval is equal to the whole remaining life. For instance, a vessel with a remaining life of 01 year shall be inspected internally after 01 years.

Personally, at the time when I was preparing for the API 510 exams, I found that this last point is counterintuitive. How we can tolerate that a pressure vessel will serve up to its whole remaining life before conducting an inspection? Would it not be risky?

Since then, I was searching for the reason for this mysterious clause. In the end, the only explanation that convinced me is that API 510 and other API standards; in many of its clauses; are based on owners’ feedback rather than empirical static formulas. That is why the API committee is one of the largest committees in the field of standardization. This rule was tested successfully for tens of years and no need to reinvent the wheel. This success may be related to the fact that construction codes adopts always a safety factor. For example in ASME VIII division 1, for tensile strength, the code requires a safety factor of 3,5. ASME BPV Section VIII, Division 2, uses a much smaller safety factor on tensile strength than Division 1 does. The safety factor is 2,4 instead.

Here it means that the required thickness is calculated not based on the actual material tensile strength but on lesser allowable stress. Hence giving a safety margin that API 510 is using to allow such a clause. This is surely a temporary measure to give owners and users more time for more radical solutions as it is clear that shutting down pressure vessels at very short intervals seems more expensive.

I-2 Double Corrosion Rate principle

to use it or even do not understand it well.

In reality, it is the same thing as the previous approach but here based on the iterative calculation of the maximum allowable Pressure. In the end, the results of the two methods are approximately the same. But the double corrosion rate principle gives a more accurate result.

When using this approach the inspector shall be careful to correct the inner radius by 2 times the corrosion rate. Actually, the inner diameter tends to be larger over time.

By correcting initially the thickness and the inner radius considering 02 times the corrosion rate the result will be automatically the remaining life/2 .

We will try to illustrate this approach via an example so the whole picture gets clearer

Below is an example of a pressure Vessel Parameter:

Symbol	Variable	Value
Di	Initial Internal Diameter	96 In
Ri	Initial Internal Radius	48 In
torg	Original Thickness	1.25 In
tcr	Current Thickness	0.92 In
S	Allowable Stress	16250 psi
E	Joint Efficiency	1
CR	Corrosion rate	0.001 In/year
tr	Retirement Thickness	0.896 In
MAWPr	Retirement MAWP	300 psi

Maximum allowable Pressure as a function of time is given by the below formula. You can see that the ASME formula for calculating MAWP is now corrected by subtracting 2 times the corrosion rate from the thickness and adding 2 times the corrosion rate to the inside radius. Where I is the incrimination of time interval since the inspection date

$MAWP(t) = \frac{S*E*tcr – 2*CR*I}{R_{i} + 2*CR*I + 0.6 *(tcr-2*CR*I)}$

Iterations give us the following result:

l	tcr-2crI	Ri +2 CRI	MAWP(t)	MAWPr
0	0.92	48	307.9172846	300
0.1	0.9198	48.0002	307.8498388	300
0.2	0.9196	48.0004	307.7823932	300
0.3	0.9194	48.0006	307.7149479	300
0.4	0.9192	48.0008	307.6475027	300
0.5	0.919	48.001	307.5800578	300
0.6	0.9188	48.0012	307.5126132	300
0.7	0.9186	48.0014	307.4451687	300
0.8	0.9184	48.0016	307.3777245	300
0.9	0.9182	48.0018	307.3102805	300
1	0.918	48.002	307.2428367	300
1.1	0.9178	48.0022	307.1753931	300
1.2	0.9176	48.0024	307.1079498	300
1.3	0.9174	48.0026	307.0405066	300
1.4	0.9172	48.0028	306.9730637	300
1.5	0.917	48.003	306.9056211	300
1.6	0.9168	48.0032	306.8381786	300
1.7	0.9166	48.0034	306.7707364	300
1.8	0.9164	48.0036	306.7032943	300
1.9	0.9162	48.0038	306.6358526	300
2	0.916	48.004	306.568411	300
2.1	0.9158	48.0042	306.5009696	300
2.2	0.9156	48.0044	306.4335285	300
2.3	0.9154	48.0046	306.3660876	300
2.4	0.9152	48.0048	306.2986469	300
2.5	0.915	48.005	306.2312065	300
2.6	0.9148	48.0052	306.1637663	300
2.7	0.9146	48.0054	306.0963262	300
2.8	0.9144	48.0056	306.0288865	300
2.9	0.9142	48.0058	305.9614469	300
3	0.914	48.006	305.8940075	300
3.1	0.9138	48.0062	305.8265684	300
3.2	0.9136	48.0064	305.7591295	300
3.3	0.9134	48.0066	305.6916908	300
3.4	0.9132	48.0068	305.6242524	300
3.5	0.913	48.007	305.5568142	300
3.6	0.9128	48.0072	305.4893761	300
3.7	0.9126	48.0074	305.4219384	300
3.8	0.9124	48.0076	305.3545008	300
3.9	0.9122	48.0078	305.2870634	300
4	0.912	48.008	305.2196263	300
4.1	0.9118	48.0082	305.1521894	300
4.2	0.9116	48.0084	305.0847527	300
4.3	0.9114	48.0086	305.0173163	300
4.4	0.9112	48.0088	304.9498801	300
4.5	0.911	48.009	304.882444	300
4.6	0.9108	48.0092	304.8150083	300
4.7	0.9106	48.0094	304.7475727	300
4.8	0.9104	48.0096	304.6801373	300
4.9	0.9102	48.0098	304.6127022	300
5	0.91	48.01	304.5452673	300
5.1	0.9098	48.0102	304.4778326	300
5.2	0.9096	48.0104	304.4103982	300
5.3	0.9094	48.0106	304.342964	300
5.4	0.9092	48.0108	304.2755299	300
5.5	0.909	48.011	304.2080962	300
5.6	0.9088	48.0112	304.1406626	300
5.7	0.9086	48.0114	304.0732292	300
5.8	0.9084	48.0116	304.0057961	300
5.9	0.9082	48.0118	303.9383632	300
6	0.908	48.012	303.8709305	300
6.1	0.9078	48.0122	303.8034981	300
6.2	0.9076	48.0124	303.7360658	300
6.3	0.9074	48.0126	303.6686338	300
6.4	0.9072	48.0128	303.601202	300
6.5	0.907	48.013	303.5337705	300
6.6	0.9068	48.0132	303.4663391	300
6.7	0.9066	48.0134	303.398908	300
6.8	0.9064	48.0136	303.3314771	300
6.9	0.9062	48.0138	303.2640464	300
7	0.906	48.014	303.196616	300
7.1	0.9058	48.0142	303.1291857	300
7.2	0.9056	48.0144	303.0617557	300
7.3	0.9054	48.0146	302.9943259	300
7.4	0.9052	48.0148	302.9268964	300
7.5	0.905	48.015	302.859467	300
7.6	0.9048	48.0152	302.7920379	300
7.7	0.9046	48.0154	302.724609	300
7.8	0.9044	48.0156	302.6571803	300
7.9	0.9042	48.0158	302.5897519	300
8	0.904	48.016	302.5223236	300
8.1	0.9038	48.0162	302.4548956	300
8.2	0.9036	48.0164	302.3874678	300
8.3	0.9034	48.0166	302.3200403	300
8.4	0.9032	48.0168	302.2526129	300
8.5	0.903	48.017	302.1851858	300
8.6	0.9028	48.0172	302.1177589	300
8.7	0.9026	48.0174	302.0503322	300
8.8	0.9024	48.0176	301.9829058	300
8.9	0.9022	48.0178	301.9154795	300
9	0.902	48.018	301.8480535	300
9.1	0.9018	48.0182	301.7806277	300
9.2	0.9016	48.0184	301.7132022	300
9.3	0.9014	48.0186	301.6457768	300
9.4	0.9012	48.0188	301.5783517	300
9.5	0.901	48.019	301.5109268	300
9.6	0.9008	48.0192	301.4435021	300
9.7	0.9006	48.0194	301.3760776	300
9.8	0.9004	48.0196	301.3086534	300
9.9	0.9002	48.0198	301.2412294	300
10	0.9	48.02	301.1738056	300
10.1	0.8998	48.0202	301.106382	300
10.2	0.8996	48.0204	301.0389587	300
10.3	0.8994	48.0206	300.9715356	300
10.4	0.8992	48.0208	300.9041127	300
10.5	0.899	48.021	300.83669	300
10.6	0.8988	48.0212	300.7692675	300
10.7	0.8986	48.0214	300.7018453	300
10.8	0.8984	48.0216	300.6344233	300
10.9	0.8982	48.0218	300.5670015	300
11	0.898	48.022	300.4995799	300
11.1	0.8978	48.0222	300.4321586	300
11.2	0.8976	48.0224	300.3647374	300
11.3	0.8974	48.0226	300.2973165	300
11.4	0.8972	48.0228	300.2298959	300
11.5	0.897	48.023	300.1624754	300
11.6	0.8968	48.0232	300.0950552	300
11.7	0.8966	48.0234	300.0276351	300
11.8	0.8964	48.0236	299.9602153	300
11.9	0.8962	48.0238	299.8927958	300
12	0.896	48.024	299.8253764	300

This can be illustrated graphically as in the below figure

The vessel’s Half remaining life is 11.7 Years (Versus 12 years if based on the thickness approach) which means that the next planned inspection shall be in 10 years.

In terms of results, there are no big differences between the two approaches but in terms of information, the second approach is very illustrative. In fact, the above figure constitutes the modeling of a pressure safety envelope up to the end of the vessel life if the corrosion rate remains the same. This can be also corrected if additional on-stream thickness measurements are conducted at regular intervals.

I-3 Half-Life or Double Corrosion Rate principles which one to use?

In general, there are no rules. The two approaches give correct results. The first approach based on thicknesses is a quick conservative tool. The second one based on the iterative calculation of MAWP is a more detailed method with more accurate results and a more useful output. There is a case where API 510 gives reference to the Double Corrosion Rate principle.

When the pressure vessel is working in corrosive service, API 510 advises correcting the thickness by considering double the corrosion rate. API 510 does not explicitly state to calculate the remaining life by this method but rather the MAWP but in the end, it is the same thing.

If we consider the same example as the one stated previously, but with the vessel working in corrosive service we will have the following (after correcting the thickness and the inner Radius by 4 times the corrosion rate:

l	tcr-2crI	Ri +2 CRI	MAWP(t)	MAWPr
0	0.92	48	307.9172846	300
0.1	0.9196	48.0004	307.7823932	300
0.2	0.9192	48.0008	307.6475027	300
0.3	0.9188	48.0012	307.5126132	300
0.4	0.9184	48.0016	307.3777245	300
0.5	0.918	48.002	307.2428367	300
0.6	0.9176	48.0024	307.1079498	300
0.7	0.9172	48.0028	306.9730637	300
0.8	0.9168	48.0032	306.8381786	300
0.9	0.9164	48.0036	306.7032943	300
1	0.916	48.004	306.568411	300
1.1	0.9156	48.0044	306.4335285	300
1.2	0.9152	48.0048	306.2986469	300
1.3	0.9148	48.0052	306.1637663	300
1.4	0.9144	48.0056	306.0288865	300
1.5	0.914	48.006	305.8940075	300
1.6	0.9136	48.0064	305.7591295	300
1.7	0.9132	48.0068	305.6242524	300
1.8	0.9128	48.0072	305.4893761	300
1.9	0.9124	48.0076	305.3545008	300
2	0.912	48.008	305.2196263	300
2.1	0.9116	48.0084	305.0847527	300
2.2	0.9112	48.0088	304.9498801	300
2.3	0.9108	48.0092	304.8150083	300
2.4	0.9104	48.0096	304.6801373	300
2.5	0.91	48.01	304.5452673	300
2.6	0.9096	48.0104	304.4103982	300
2.7	0.9092	48.0108	304.2755299	300
2.8	0.9088	48.0112	304.1406626	300
2.9	0.9084	48.0116	304.0057961	300
3	0.908	48.012	303.8709305	300
3.1	0.9076	48.0124	303.7360658	300
3.2	0.9072	48.0128	303.601202	300
3.3	0.9068	48.0132	303.4663391	300
3.4	0.9064	48.0136	303.3314771	300
3.5	0.906	48.014	303.196616	300
3.6	0.9056	48.0144	303.0617557	300
3.7	0.9052	48.0148	302.9268964	300
3.8	0.9048	48.0152	302.7920379	300
3.9	0.9044	48.0156	302.6571803	300
4	0.904	48.016	302.5223236	300
4.1	0.9036	48.0164	302.3874678	300
4.2	0.9032	48.0168	302.2526129	300
4.3	0.9028	48.0172	302.1177589	300
4.4	0.9024	48.0176	301.9829058	300
4.5	0.902	48.018	301.8480535	300
4.6	0.9016	48.0184	301.7132022	300
4.7	0.9012	48.0188	301.5783517	300
4.8	0.9008	48.0192	301.4435021	300
4.9	0.9004	48.0196	301.3086534	300
5	0.9	48.02	301.1738056	300
5.1	0.8996	48.0204	301.0389587	300
5.2	0.8992	48.0208	300.9041127	300
5.3	0.8988	48.0212	300.7692675	300
5.4	0.8984	48.0216	300.6344233	300
5.5	0.898	48.022	300.4995799	300
5.6	0.8976	48.0224	300.3647374	300
5.7	0.8972	48.0228	300.2298959	300
5.8	0.8968	48.0232	300.0950552	300
5.9	0.8964	48.0236	299.9602153	300

The Half Remaining life is estimated to 5,8 Years, thus the next internal inspection shall be in 5,8 years not 10 years as previously stated for non-corrosive service.

So personally I consider Double Corrosion Rate approach more adequate for authorized inspectors to adopt.

II Corrosion Rate Selection:

In reality, the remaining life calculation method is not as critical as the corrosion rate calculation and selection. The use of an erroneous corrosion rate will automatically impact the inspection result.

To make sure that the calculated corrosion rate is correct the authorized inspector shall check the following:

Consult with operation personnel and if required with a corrosion specialist to check if the vessel was subject to change in service and or design in the past that can affect the corrosion rate.
Analyze statistically the thickness measurement records to characterize internal thinning.
Apply the principle of API 510 section 7 when conducting averaging of the thickness readings or the principle of thickness profiling stated in API 579 part 5.

II-1 Effect of Service/Design Change on Corrosion rate selection

API 510 defines two types of Corrosion rates to be used Short Term Corrosion rate and Long Term Corrosion Rate. It is a very simplistic approach to state that the higher of these two rates shall be used.

For instance, a change in the process can affect the corrosion rate by increasing or decreasing it. The approximate date of such change shall be estimated via consulting with operation personnel. Such an event can be suspected if a notable change in the corrosion rate tendency is observed from previous inspection reports. If confirmed the long-term corrosion rate shall be calculated from that date of service change.

The changing of a pressure vessel part material of construction is also the essential information to be gathered and checked otherwise inaccurate results will be generated.

II-2 Statistical analysis of Thickness Measurement

One of the most efficient ways (of course after visual inspection) to identify the type of internal thinning is by analyzing the result of thickness measurements statistically.

As a rule of thumb, If the COV of the thickness reading population minus the Future Corrosion Allowance (FCA) is less than 10%, then the general metal loss is defined to be uniform and the average thickness can be computed directly from the population of thickness readings.

If the COV is greater than 10%, then the use of thickness profiles is required to determine the average thickness. API 510 gives many criteria on how to average localized thinned areas.

If the COV test for point thickness readings is greater than 10%, then the general metal loss is defined to be non-uniform and the use of thickness profiles is required. An inspection grid covering the region of metal loss is typically required to determine the extent of the damage.

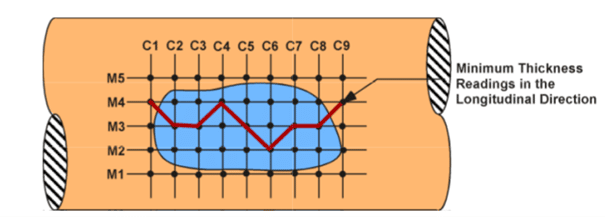
In the end, what I wanted to say here is that corrosion rate selection and related remaining life calculation is a critical activity that API 510 inspectors shall not neglect. Inspectors shall have a solid understanding of their choices and estimations.

There are many other related topics that can be discussed also here but I prefer to detail them in other articles.

Ali Sassi

API 510 / API 653 inspector

If you have any API 510 questions do not hesitate to contact us.

we offer also API 510 training sessions to prepare candidates to pass the API exam with our partner WTC. If you would like to learn more visit http://www.wtctunisie.com